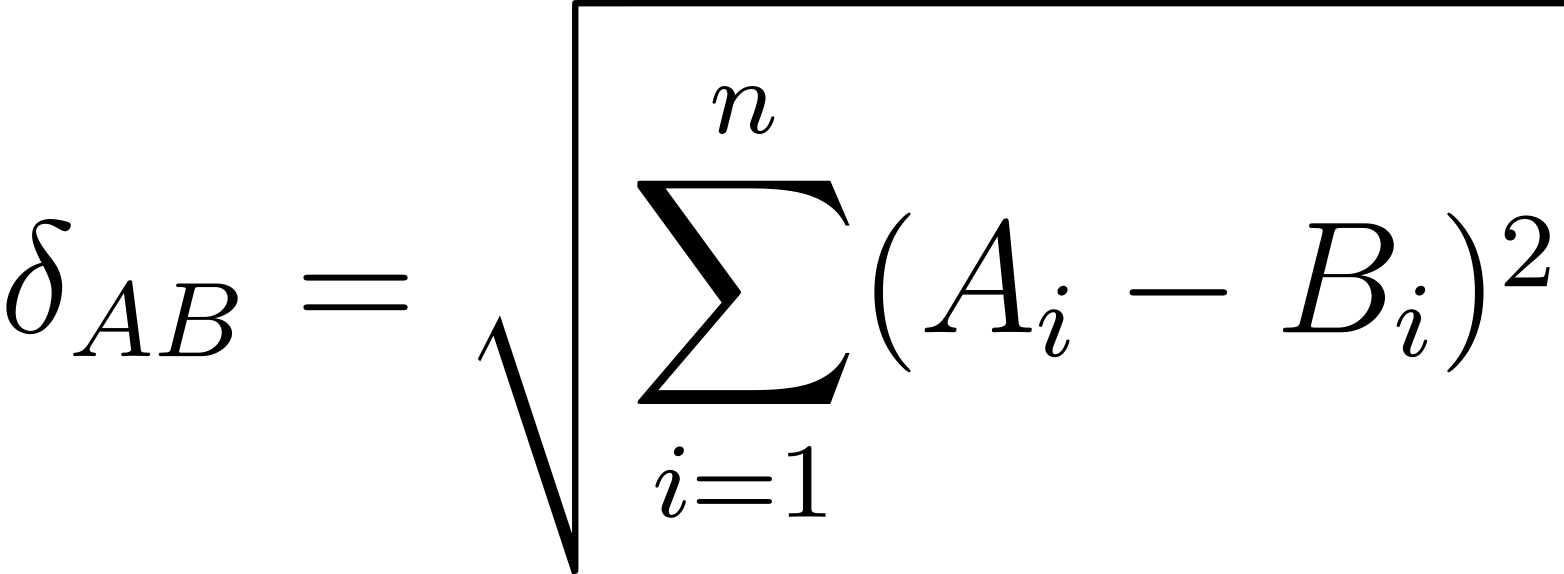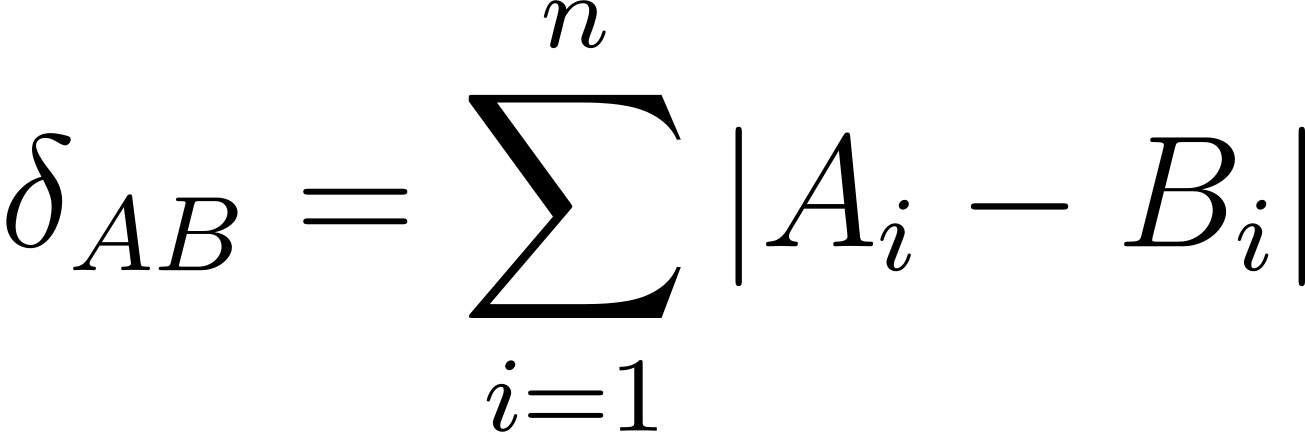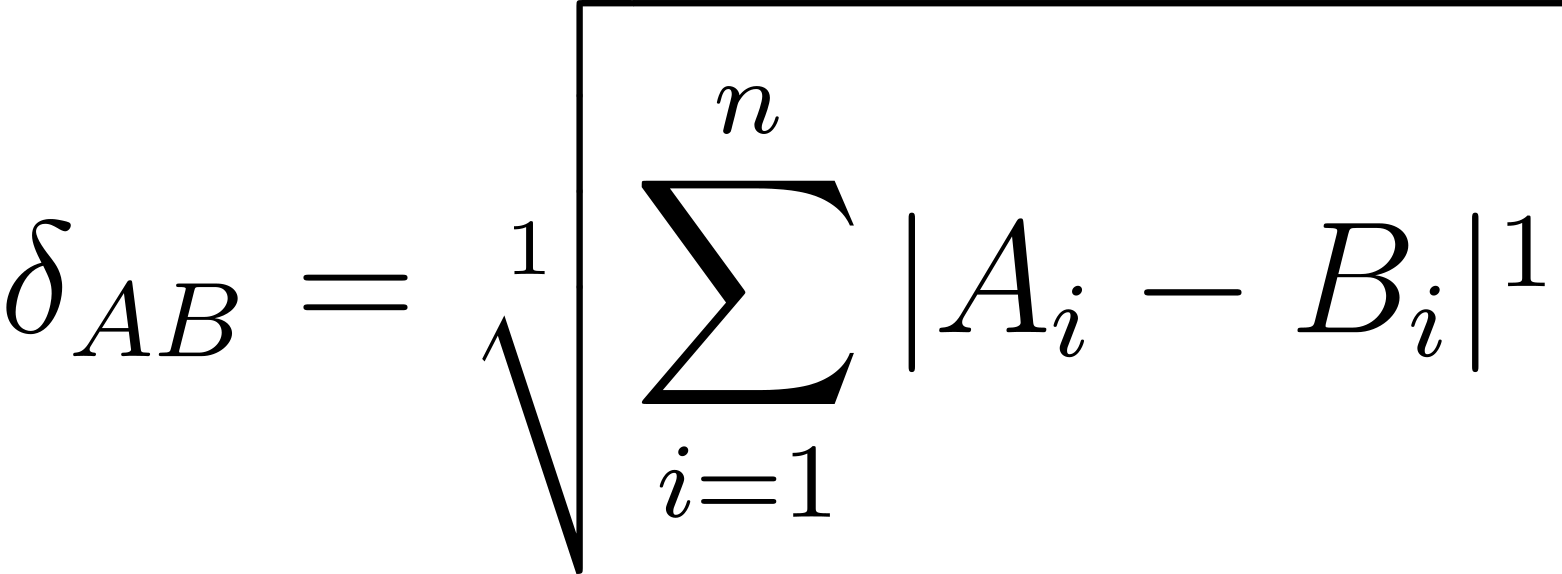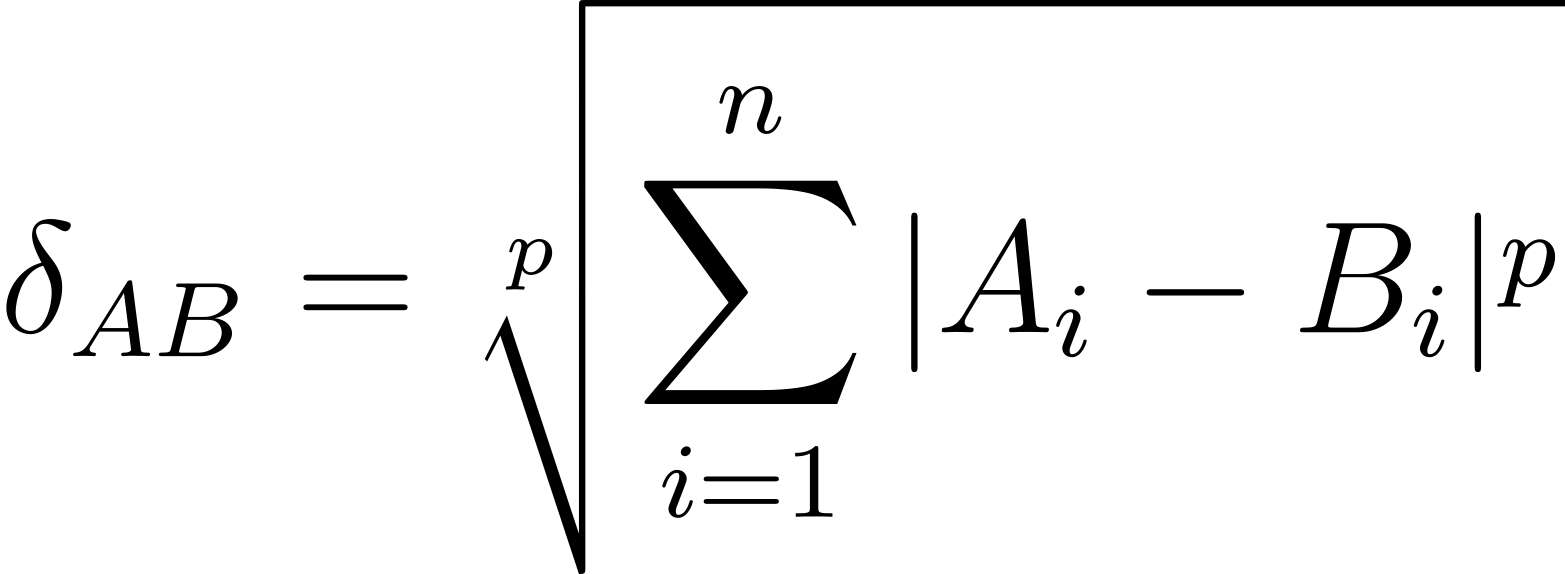Manhattan, Euclidean, and their Siblings: Exploring Exotic Similarity Measures in Text Classification

1. Abstract

In this paper, we empirically assess a continuum of similarity measures that share mathematical properties with two classical distance metrics, namely Manhattan and Euclidean. In a systematic experiment, we discover the relation between a given distance and the number of input features.

Keywords: authorship attribution, stylometry, distance metrics, L1 norm, L2 norm

2. Introduction

Similarity measures are routinely used in the realm of text analysis, mostly in solving classification and/or clustering tasks. Usual applications include authorship attribution, genre analysis, intertextuality detection, register analysis and so forth. A vast majority of these methods rely — explicitly or not — on some notion of similarity that is to be inferred from the analyzed documents (texts); a good share of the methods define the similarity as a form of a geometrical distance in a multidimensional space. Despite the impressive power of recent applications of deep learning in text classification (Benzebouchi et al. 2018; Gómez-Adorno et al. 2018), at least in scenarios with large amounts of training data, distance-based approaches are still considered competitive, especially when the number of classes is relatively high (Luyckx / Daelemans 2011).

However, the main reason for exploring distance-based similarity measures — rather than deep learning models with billions of parameters — they are inherently interpretable and the notion of distance is relatively easy to grasp. Consequently, methods relying on distances prove attractive in helping understand the underlying factors responsible for better or worse classification results. In the present paper we follow the above reasoning. Specifically, our aim is to provide a deeper understanding why two texts written by the same author tend to be similar, rather than to benchmark recent neural network systems.

Even if the list of known distance measures includes 5,000 or so items (Moisl 2014), only a few of them are actually used in text analysis. Traditionally, three main distances should be mentioned: Manhattan, Euclidean, and Cosine. It is true that many other measures are also worth mentioning (Kocher / Savoy 2017; Savoy 2020), among which the Minmax distance is probably worth a special attention (Kestemont et al. 2016), nevertheless the said three distances can be considered foundational. Several other measures are modifications or derivatives of these three. The most remarkable modification is Delta (Burrows 2002), being in fact the Manhattan measure applied to scaled (z-scored) frequencies. Other ways of scaling the dataset, such as using ft-idf weighting, have also been explored (Nagy 2023). Also, replacing the Manhattan kernel in Delta with Euclidean measure has been suggested as potentially a more natural solution (Argamon 2011; Moisl 2014). Also, there is some evidence that replacing the original kernel with the Cosine metrics improves performance of the classical Burrows’s distance (Jannidis et al. 2015). Interestingly, several standard classifiers and/or dimensionality reduction methods, such as k-NN, SVM, or PCA, rely on an Euclidean kernel. There has been no systematic study whether such a switch from the Manhattan to the Euclidean space affects the classification.

3. L1 and L2 norms

Euclidean distance between any two texts represented by two points A and B in an n-dimensional space can be defined as:

where A and B are the two documents to be compared, and 𝐴 _𝑖, 𝐵 _𝑖 are the scaled (z-scored) frequencies of the i-th word in the range of n most frequent words.

Manhattan distance can be formalized as follows:

which is equivalent to

The above notation, somewhat superfluous if not odd, makes it easy to realize that both Euclidean and Manhattan are in fact siblings. Because their only difference is the power, either 1 or 2, they are usually referred to as the L1 norm and the L2 norm (to denote the Euclidean and the Manhattan distance, respectively).

The observations made so far can be further generalized. It is straightforward to observe that the said two distances belong to an infinite family of (possible) distances that can be formulated as follows:

where 𝑝 is both the power used in the equation and the degree of the root.

Consequently, apart from the commonly known L1 and L2, one can think of other norms, e.g. L4 or L15. The generalization can go even further. Since the power doesn’t need to be a natural number, we can easily imagine norms such as L1.01, L3.14159, L1¾ etc. Mathematically, 𝑝 < 1 doesn’t satisfy the formal definition of a norm, yet still, one can easily imagine a dissimilarity L0.5 or L0.0001. In fact, Evert et al. (2017) compared Lp norms and other adjustments in text clustering experiments. For the sake of the present paper it is important to realize that 𝑝 is a continuum, where both 𝑝 = 1 and 𝑝 = 2 (for L1 and L2, respectively) are but two specific points in this continuous space, and 𝑝 is a method’s hyperparameter to be set or possibly tuned. If so, an obvious research question can be formulated: how do the norms from a wide range beyond L1 and L2 affect text classification?

In order to address this question, a systematic comparison of a series of distances covering the range L0.1, L0.2, L0.3 etc. all the way to L10 was conducted. As a text classification task, a few authorship attribution benchmark problems were chosen.

4. Data and Method

To address the above research question, four datasets were used: (1) a collection of 99 English novels by 33 authors, (2) a collection of 99 Polish novels by 33 authors, (3) a collection of 28 books by 8 American Southern authors: Harper Lee, Truman Capote, William Faulkner, Ellen Glasgow, Carson McCullers, Flannery O’Connor, William Styron and Eudora Welty, and (4) a somewhat random collection of 26 books by 5 authors: J.K. Rowling, Harlan Coben, C.S. Lewis, and J.R.R. Tolkien. The first two corpora are posted on our GitHub repository, whereas the other two are available in the form of tables of relative frequencies, in the stylometric package ‘stylo’ (Eder et al. 2016).

A supervised classification experiment was designed, with leave-one-out cross-validation scenario. In each of the cross-validation folds, 100 independent bootstrap iterations were performed, each of them computing an independent test for authorship on 50% randomly selected input features (most frequent words). The procedure was then systematically repeated for the ranges of 100, 200, 300, …, 1000 most frequent words. Needless to say, the entire experimental setup was then repeated iteratively for subsequent distance measures: L0.1, L0.2, …, L10. The performance in each of the iterations within iterations was evaluated using standard tools, namely accuracy, recall, precision, and the F1 scores. For the sake of simplicity, all the values reported below are the F1 scores.

5. Results

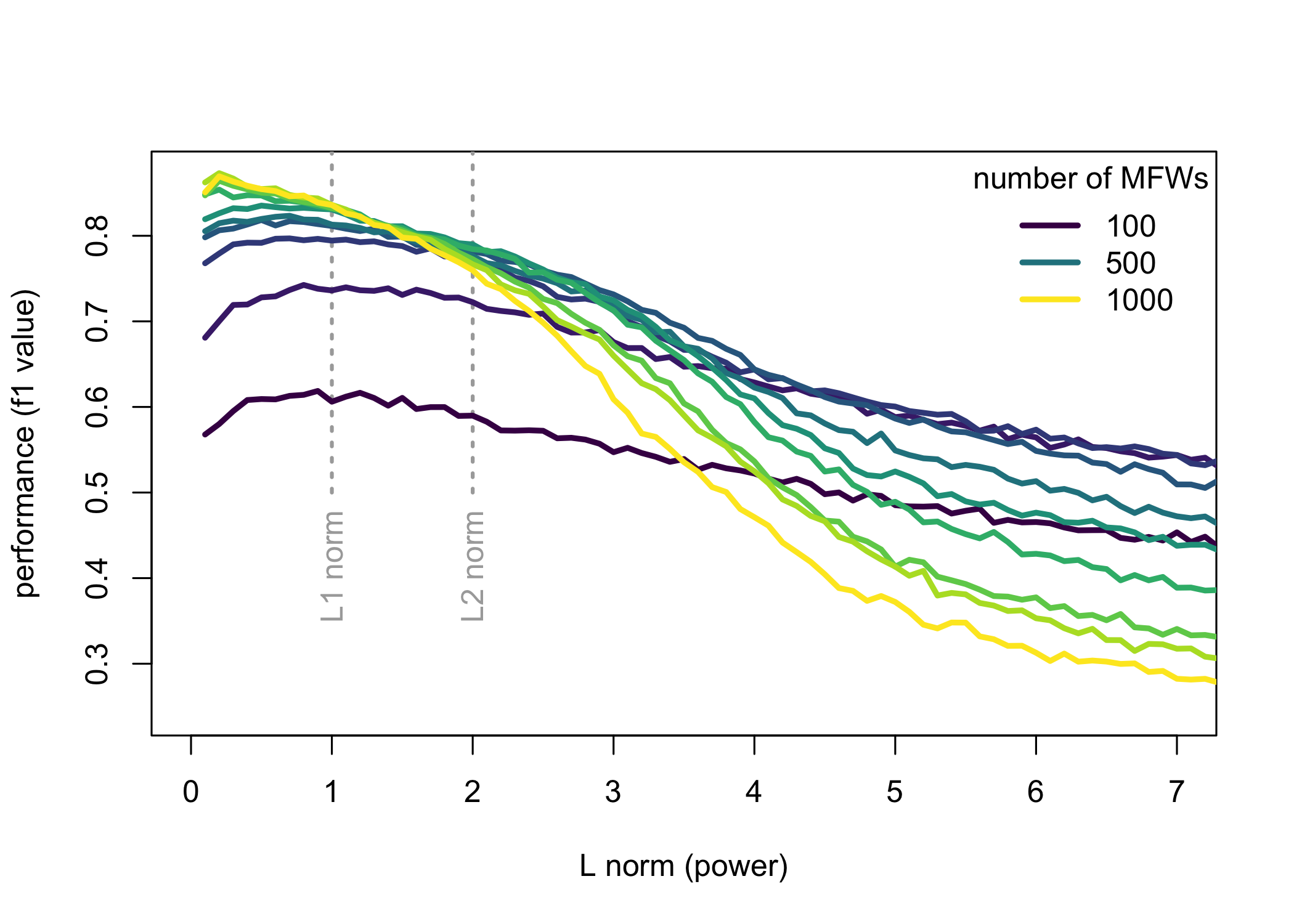
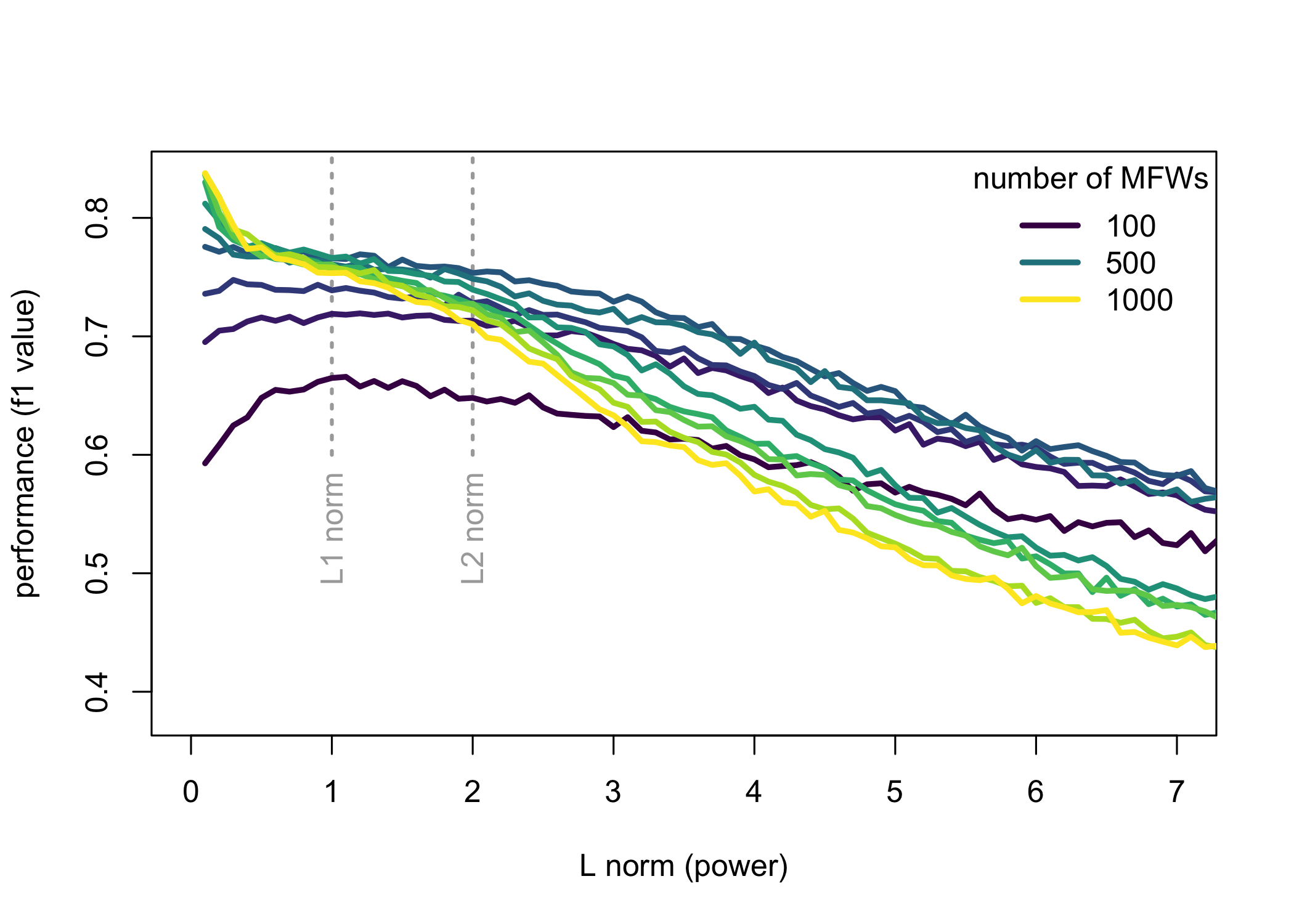
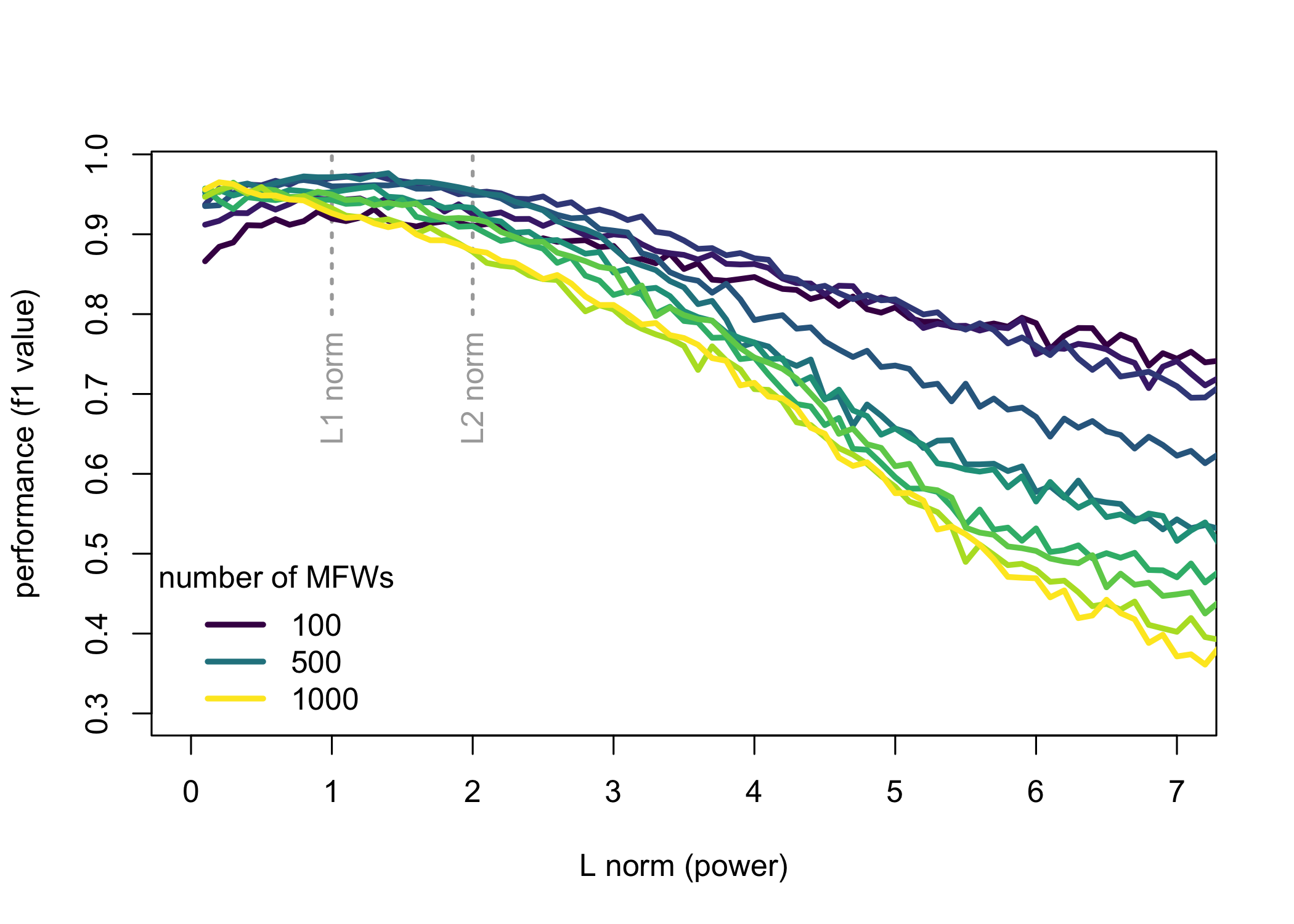
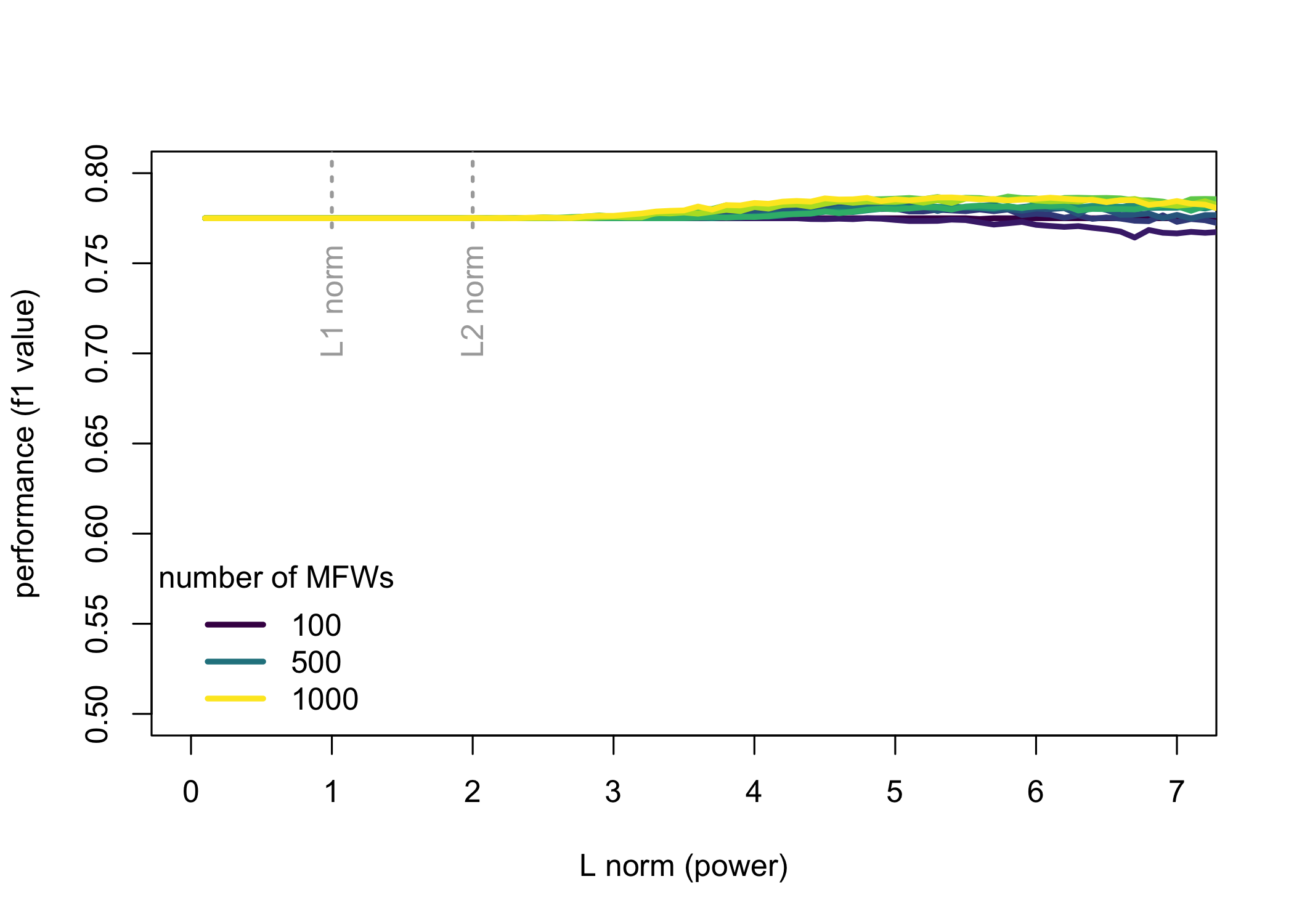
The results of the four experiments are shown in Figs. 1–4. With the exception of the fourth corpus – which turned out to be an easy task for the classifier – all the other corpora behaved in a similar way. A few general observations can be made. Firstly, a bigger picture shows that L2 might occasionally outperform L1, but in principle, norms of a higher power are always worse than these with a lower p. Secondly, the continuum going below L1 suggests that the performance continues to increase even in the realm that does not satisfy a formal definition of a norm. For the English corpus (Fig. 1) the best results are obtained using L0.3 metrics, whereas for the Polish corpus (Fig. 2) the optimal value goes even further to L0.1. Thirdly, a known difference in performance between longer or shorter feature spaces (say, for 100 vs. 1,000 most frequent words) is confirmed once again. However, we can also see a different sensitivity to the chosen distance metrics: while long vectors of features yield significantly better results than shorter ones, at the same time large feature spaces are much more dependent on the fine-tuned distance measure.

[Page]

Figure 1: The performance (F1 scores) for a benchmark corpus of 99 English novels, with the Delta classifier. The current distance measure is shown on the x axis (L1 norm is the Manhattan distance, and L2 the Euclidean distance).

Figure 2: The performance (F1 scores) for a benchmark corpus of 99 Polish novels, with the Delta classifier.

[Page]

Figure 3: The performance (F1 scores) for a benchmark corpus of 28 novels by 8 American Southern authors.

[Page]

Figure 4: The performance (F1 scores) for a benchmark corpus of 26 novels by 5 fantasy writers.

6. Conclusions

In the current study, a systematic comparison of distance measures was conducted. The experiments addressed not only the Manhattan (L1) and the Euclidean (L2) metrics but also a continuum beyond the L1 and L2 norms, covering the range from L0.1 to L10. The results suggested that metrics with lower p generally outperform higher-order norms. Also, it turned out that the parameters (feature vectors) that yield the best results (here: long vectors of most frequent words) are at the same time the most sensitive to the choice of the distance measure. A similar behavior has been observed in a study addressing systematic errors in stylometry (Eder, 2012).

In the outlook, while metrics for p < 1 are not technically distances (then, neither is the Cosine distance), their properties seem helpful in practice – they also explain some observations and hypotheses made previously (Evert et al. 2017). These properties are:

1. small p makes it more important for two feature vectors to have fewer differing features (rather than smaller differences among many features),

2. small p amplifies small differences (important, e.g., for low-frequency features in distinguishing between 0 difference – for two texts lacking a feature – and a small difference),

3. for p < 1 the nearest-neighbor decision boundaries can become disconnected (and effectively more fine-grained).

Although the classic formulation of the curse of dimensionality states that differences in the distances become indiscernible in high dimensions making long feature vectors not useful, e.g., in nearest neighbor search (and Delta is a nearest-neighbor classifier), in practice machine learning can take advantage of peculiarities of feature distributions which break some assumptions. Small p norms might be one way of effectively utilizing long feature vectors.

7. Acknowledgments

The study was conducted as a part of the “Large-Scale Text Analysis and Methodological Foundations of Computational Stylistics project” (SONATA-BIS 2017/26/E/HS2/01019) funded by the Polish National Science Center (NCN). JO’s venture has been made possible thanks to the funding provided by the Jagiellonian University’s Flagship Project “Digital Humanities Lab”. The code and the datasets to replicate the experiments presented in this study are posted on GitHub repository: https://github.com/computationalstylistics/beyond_Manhattan.