Theorizing risk attitudes and rationality using agent based modeling

This poster presents results from applying agent-based modeling to an exploration of risk attitudes and rational decision making in the context of group interaction. We are also interested in the place of agent-based modeling and computational philosophy within the computational humanities. Computational philosophy has not typically been included in Digital Humanities; computational work has been done using philosophy texts as a source for analysis (Kinney 2022; Malaterre et al. 2021; Fletcher et al. 2021; Zahorec et al. 2022), but there are few examples of philosophical arguments being made based on computation (Zahorec et al. 2022). Modeling is largely accepted as a computational humanist method (McCarty 2004; So 2022), but typically models are based on data rather than designed simulations as a method analogous to a thought experiment (Mayo-Wilson / Zollman 2021). Agent-based modeling is not as common in computational humanities, but we are interested in its potential; for instance, see work modeling correspondence networks to better understand lost information and biases in correspondence data sets (Buarque / Vogl 2023), or work simulating past human societies (Romanowska et al. 2021).

Our project explores Lara Buchak’s theory of risk-weighted rational decision making by extending it to the context of group populations and interactions. Buchak has proposed risk-weighted expected utility maximization, which incorporates individual risk attitudes into the standard expected utility (EU) calculation based on utility and probability of outcomes (Buchak 2017). This theory provides an explanation for differences of behavior seen in human populations, while still allowing those different choices to be rational. Buchak’s theory has previously only been applied to individual decision making; our work uses agent-based modeling to develop and analyze simulations which incorporate a variety of risk attitudes (risk avoidance and risk seeking) into game theoretic interactions.

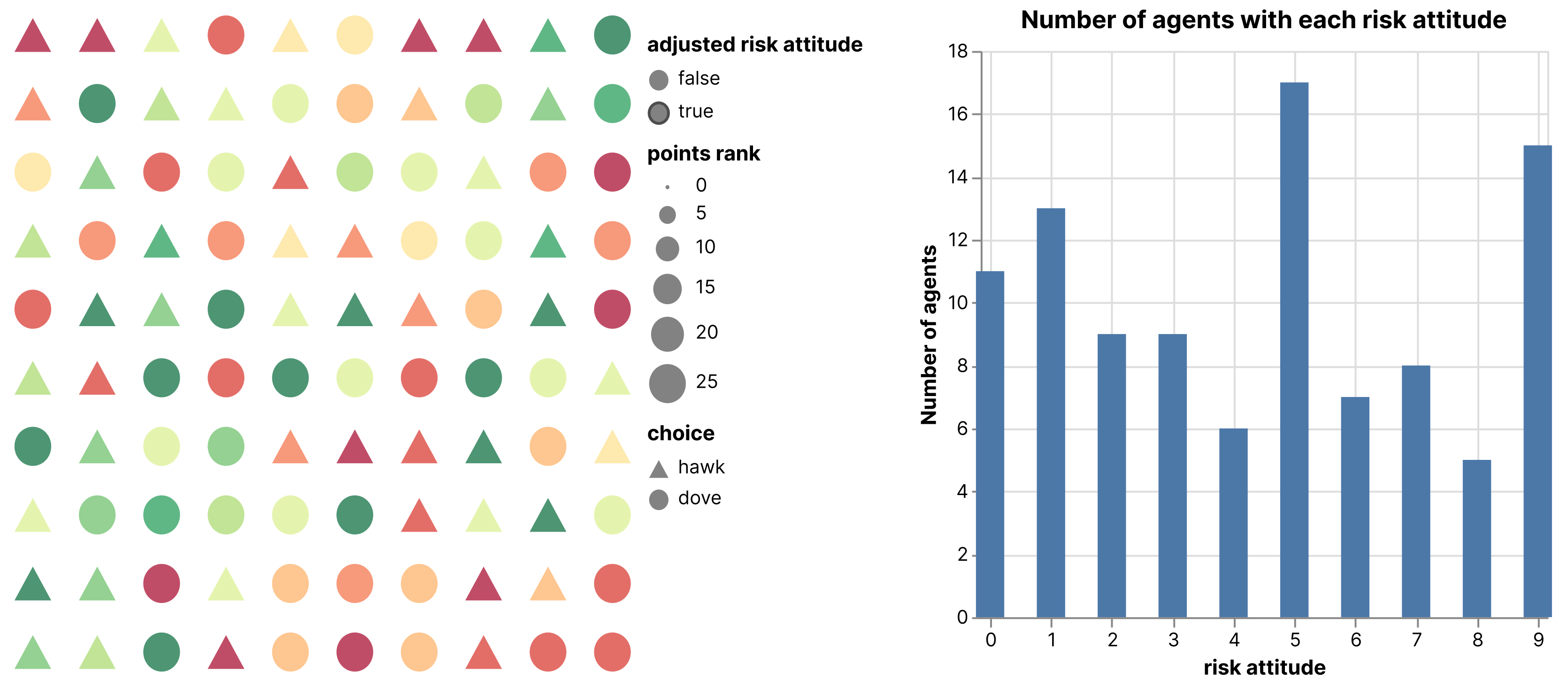
This project is a collaboration between a philosopher and a research software engineer; we have worked together to develop simulations that implement agents with risk attitudes making risky choices. ¹ This presentation focuses on results from an implementation of a hawk/dove game with multiple risk attitudes and risk attitude adjustment. In the hawk/dove game cooperation, or playing dove, is better for the population, but acting aggressively, or playing hawk, is better for an individual if they are in a neighborhood of doves. To set up the game, we place agents on a grid and have them play against each of their neighbors, and accumulate payoffs based on the success of their plays (Figure 1).

Figure 1. Example starting setup for hawk/dove game with multiple risk attitudes. Left: agent grid with random risk attitudes; a diverging color scheme indicates risk attitude: reds and oranges are risk seeking agents and greens are risk avoidant. Right: initial distribution of risk attitudes.

We define risk attitudes 0 through 9, where that number corresponds to the minimum number of neighbors playing dove for an agent to play hawk. An agent with risk attitude 0 is most risk seeking and always plays hawk; an agent with risk attitude 1 will play hawk if at least one neighbor plays dove; an agent with risk attitude 9 always takes the safe choice and plays dove; an agent with risk attitude 4 or 5 is risk neutral (breaking ties in different ways), which corresponds to expected utility. In this simulation we randomly set agent initial risk attitudes, and then every ten rounds agents compare their payoffs with their neighbors and adopt the most successful risk attitude in their neighborhood. The simulation is coded to stop once risk attitude adjustments stabilize (Figure 2).

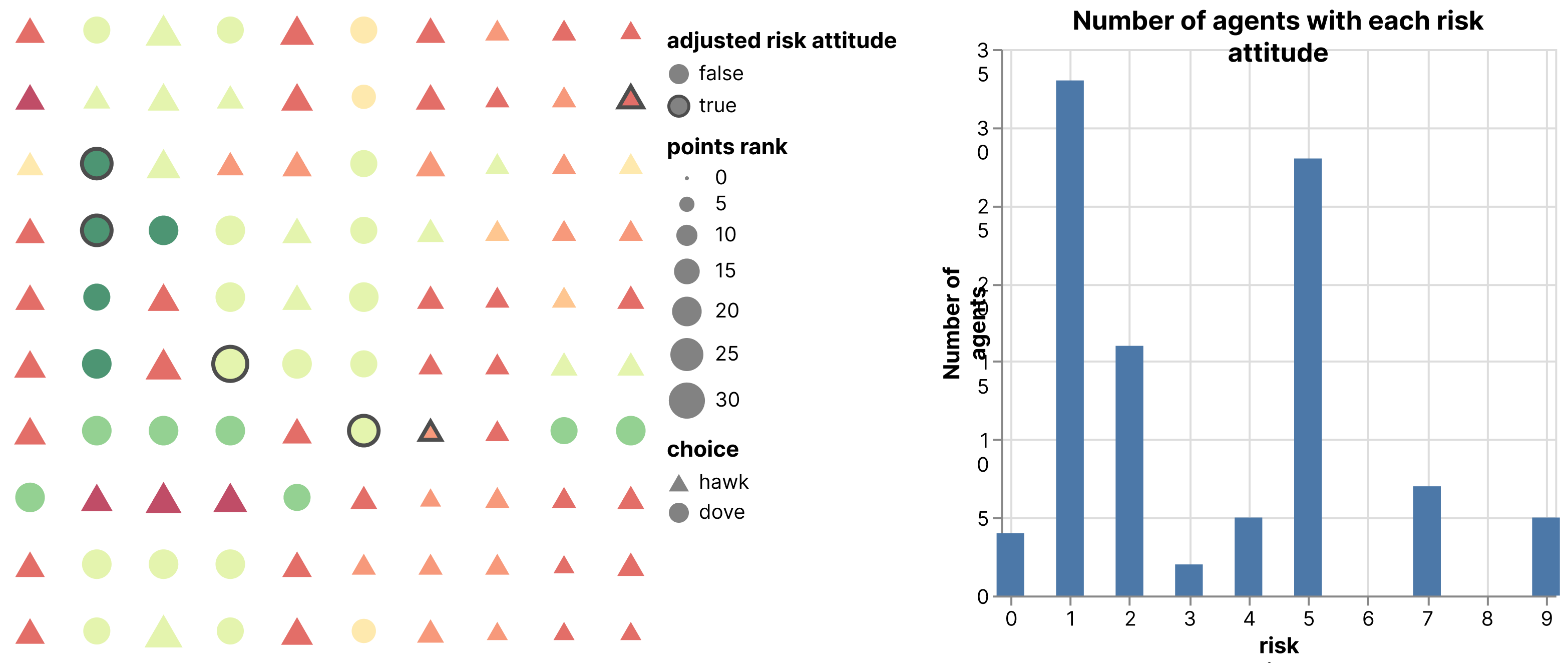
Figure 2. Example stable end state for hawk/dove game with multiple risk attitudes. Left: agent grid with adjusted risk attitudes. Right: bar chart indicating the distribution of risk attitudes across all agents after adjustments. This run ended up with large portions of the population risk inclined and risk neutral, with a few agents remaining risk avoidant.

We define 13 different population states based on primary and second majority of risk averse, risk inclined, or risk moderate, and analysis of over 1 million runs indicate that while it’s more likely to stabilize with the population having become majority risk inclined, that is not the only outcome; we also see cases where the population stabilizes as risk neutral, risk avoidant, and many cases with no clear majority (Figure 3). This diversity of stable populations provides support for the argument that no one risk attitude is uniquely rational, but rather that risk attitudes are conventional. This matches what we observe in the real world: that different populations have different risk attitudes.

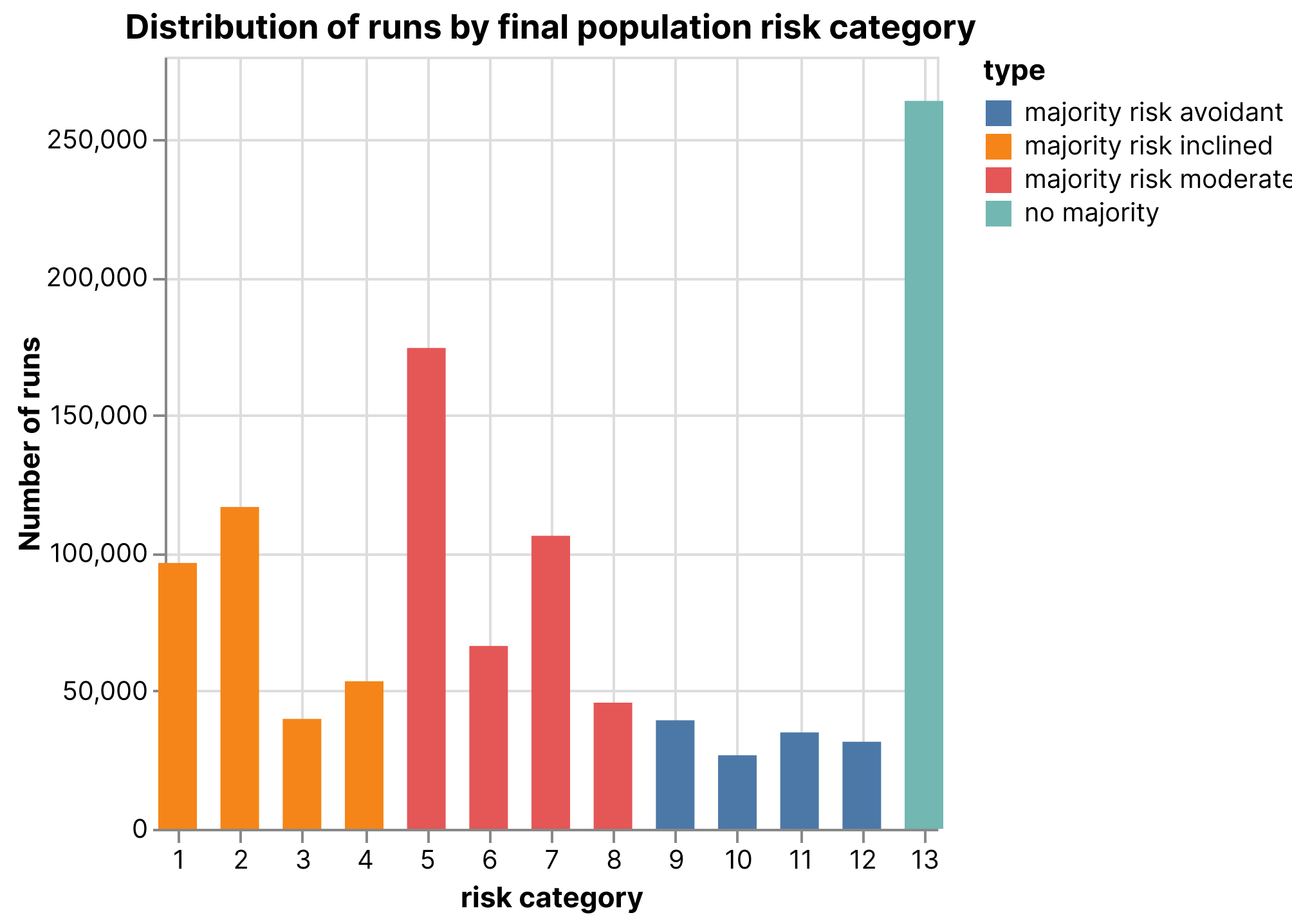
Figure 3. Distribution of population category types on over a million runs of the hawk/dove simulation.

Our simulations include numerous parameters to vary grid size; adjustment frequency, strategy, and wealth comparison; neighborhood sizes for observing previous choice, playing against, and comparing payoffs for adjusting risk attitudes; and different distributions for initializing risk attitudes. Analysis of parameters and adjusted risk attitudes shows that the strongest correlations are the initial distribution of risk attitudes, which tend to be preserved (Figure 4).

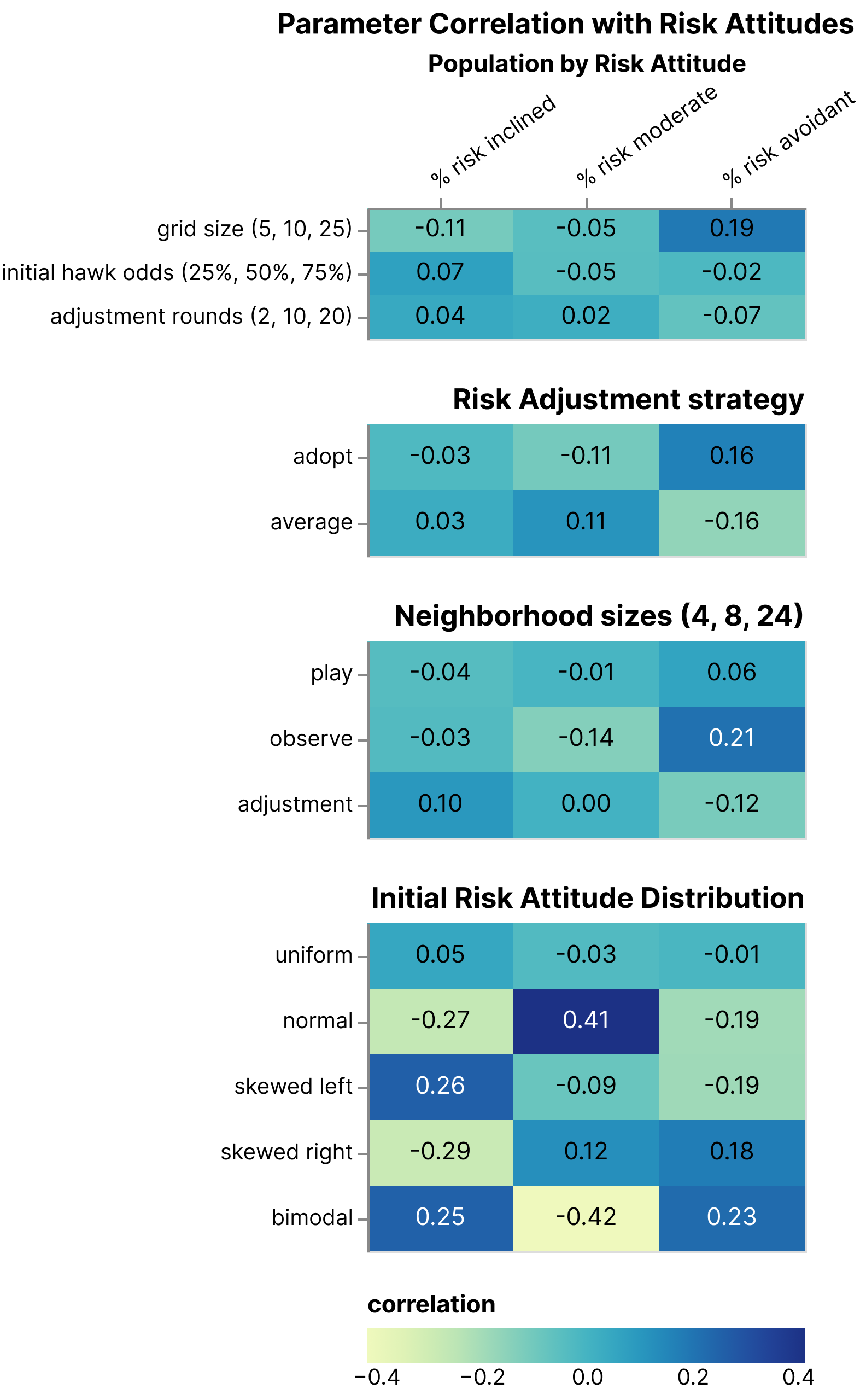
Figure 4. Correlation analysis of simulation parameters with final population risk attitudes on over a million runs of the hawk/dove simulation.