Micro- and Macroanalytical Perspectives on Knowledge Transmission in German-Language Plays (1740–1910)

1. Introduction

When Oedipus in Sophocles’ eponymous play finally recognizes the intricate family relations that lead to the play’s central dramatic conflict, there is no turning back: “If there is any ill worse than ill,/ that is the lot of Oedipus”, he summarizes the consequences of his own actions (Sophocles 1971, p. 71, v. 1365–1366). For Aristotle, Sophocles’ Oedipus the King presents the prototypical case of recognition, as it is “ensuing from the events themselves” (Aristotle 1995, p. 87). Recognition is, according to Aristotle, one of the central structural components regarding the effect of a play on the audience. He defines recognition as a “change from ignorance to knowledge, leading to friendship or to enmity, and involving matters which bear on prosperity or adversity” (Aristotle 1995, p. 65).

As – not only – the example of Sophocles’ Oedipus and Aristotle’s Poetics show, the characters’ knowledge about family relations and the knowledge transmission of family relations throughout a play are oftentimes central to developing the plot or the dramatic conflict (cf. Kiss 2010, 507–525). Manfred Pfister argues that the level of information in the internal and external communication system of a play constantly varies. This “discrepant awareness” of dramatic characters and the audience has even been labelled as the “very essence of the dramatic” (Pfister 1988, p. 49; cf. Dürrenmatt 1976, p. 75). The level of awareness is, thus, largely understood to be a central element of both tragic tension and comedic humor (cf. Anz 1998, pp. 150–169, Muny 2008 and Horstmann 2018, pp. 184–209).

Building on the outlined suppositions we have systematically annotated the transmission of knowledge – understood in a broad sense – ¹ in 30 German-language plays from the 18th, 19th and early 20th centuries (cf. Andresen et al 2024). We restricted the manual annotations to the domain of knowledge about character relations with a focus on family relations. ² In this paper, we present two approaches to model our data in light of typical research questions of computational literary studies (CLS). Firstly, we suggest utilizing our data to create character networks, where the annotated knowledge transfers are used to specify the interactions (edges) between characters (nodes). Mathematical network metrics can then be used to calculate the centrality of characters and to quantitatively compare them with characters of other plays. This yields a macroanalytical perspective on drama history. The data also enables us to contrast co-presence-based character networks ³ with networks based on knowledge transmission. Secondly, we propose to model our data as a knowledge graph, where each individual character’s level of awareness regarding her or his knowledge is represented throughout the play. This microanalytical perspective relates to ideas of cognitive literary studies (cf. Nünning 2014), namely that literary characters build theories of mind about each other.

2. Related Work

Character relations of dramatic texts have gained a lot of attention in CLS in the last ten years or so. Most notably, social network analysis has been used to model character relations and character interactions from a structural point of view (cf. Moretti 2011, Trilcke 2013, Lee/Lee 2017, Trilcke 2022), e.g., to detect the protagonist of a play (cf. Fischer et al 2018) or to assess the communicative strength of characters (cf. Krautter/Vauth 2022). In most of these cases, the co-presence of characters serves as basis to create the networks (cf. Labatut/Bost 2019, 14). Network analysis has been complemented by (semi-) automatic approaches to extract character relations from a play’s dramatis personae (cf. Wiedmer/Pagel/Reiter 2020, 194–200). Looking beyond the highly structured nature of plays, several proposals have been made to also focus on the semantic dimensions when analyzing character relations. Eric Nalisnick and Henry Baird, for instance, suggest making use of sentiment analysis to establish a character’s enemies and allies (2013a, 479–483) and to create sentiment-based character networks to model positive and negative relations between characters (2013b, 758–762).

3. Annotation Scheme

Our dataset ⁴ aims at tracking the distribution of knowledge about character relations through manual annotation. In total, we annotated 1277 text passages of 30 plays that have a combined size of 736,808 tokens. We retrieved the plays from the German Drama Corpus (Fischer et al 2019) in the TEI-XML format. Table 1 shows an overview of the annotated plays in our corpus. We selected them manually to cover a broad spectrum of different literary periods, different genres (tragedies, comedies as well as libretti), and female authors such as Karoline von Günderrode and Johanna von Weißenthurn.

For the annotation process we limited ourselves to family relations ( parent_of(A, B), child_of(B, A), siblings(B, C), ...), love relations ( in_love_with(B, D), engaged(B, D), spouses(B, D), ...) questions of identity ( identity(A, E), has_name(A,’name’)) and death ( dead(A), murderer_of(B, A)). In addition to the character relations, the annotations contain information about source and target of each knowledge transmission, so that the following tag structure results: transfer(SOURCE, TARGET, KNOWLEDGE, ATTRIBUTES). SOURCE represents the character that passes on the knowledge, TARGET is one or several characters (or the audience) that accumulates the knowledge, and KNOWLEDGE specifies the given information. Optional attributes allow certain specifications, e. g., if the information is a lie or still uncertain (for details see Andresen et al 2021, in German). All 30 plays have been annotated independently by two annotators. Issues and difficulties were discussed in several steps before creating a finalized version.

Table 1: List of plays included in our annotated corpus.

4. Comparing mathematical network metrics in knowledge networks

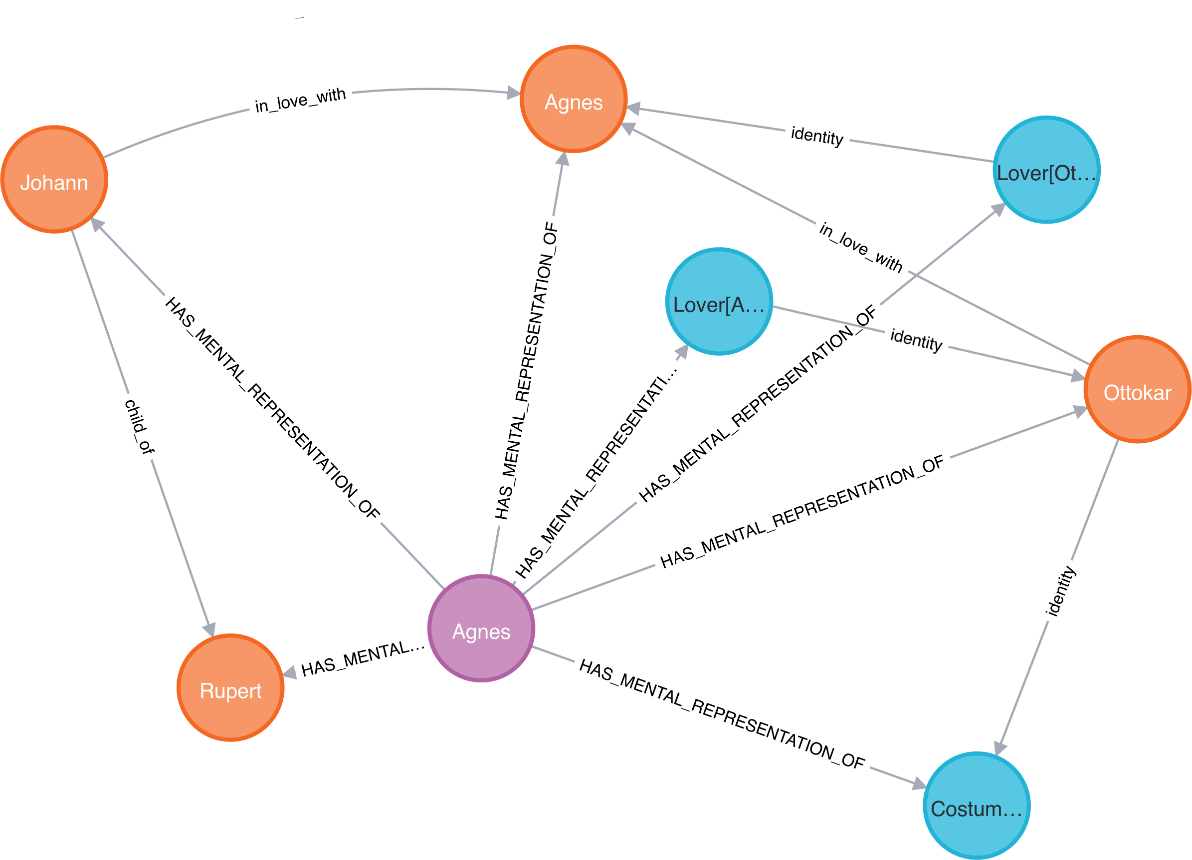
To create knowledge networks, we make use of our annotation data. Characters that are SOURCE or TARGET of a knowledge transmission are represented as nodes. Figure 1 depicts an example of such a network. The network visualizes the knowledge transmissions in Heinrich von Kleist’s tragedy Die Familie Schroffenstein (1803). As we identify both SOURCE and TARGET in our annotation data, it is possible to create a directed and weighted network. Although the relations of the knowledge transfers are not specified, the network of Die Familie Schroffenstein still offers an interesting perspective on the play. None of the main characters is at the center of the network. Instead, it is Rupert’s natural child Johann, who throughout the play has fallen into madness. The weighted edges also showcase the close proximity of the lovers Agnes and Ottokor, whose gradually developing relationship is at the center of the tragic conflict. ⁵

Figure 1: Knowledge network of Die Familie Schroffenstein.

To gain a macroanalytical perspective, we have calculated three common centrality metrics for all 30 plays in our corpus: degree, betweenness centrality, and eigenvector centrality. ⁶ Table 2 (Appendix) gives an overview and lists the average and maximum values of these metrics. While the limited number of plays does not (yet) ⁷ allow to look at possible diachronic trends, there are insights to be gained. In some cases, the maximum degree surpasses the number of characters. There are at least two reasons for this: Firstly, the networks are directed. A character’s maximum degree therefore combines in- and out-degree. Secondly, knowledge transmissions are not limited to characters that are actively performing on stage, as letters or off-stage characters can be the SOURCE of a transfer and the audience or unknown characters can be the TARGET. Another striking observation concerns the maximum (sd = 23.03) and average (sd = 3.55) betweenness centrality, as they both fluctuate pretty heavily.

To follow this second observation up with a more substantial analysis, we computed the same metrics for the corresponding co-presence networks and compared the values. Figure 2 shows boxplots for the average degree, normalized average degree, ⁸ betweenness and eigenvector centrality values in our corpus of 30 plays. As becomes visible throughout all metrics, the medians of the knowledge networks are considerably lower than those of the co-presence networks. The values, however, are not only lower, but the variance is also less pronounced. This holds also true for the betweenness centrality. From a theoretical point of view, one might wonder, whether the lower values simply correspond to the – in most cases – smaller sizes of the knowledge networks. This needs further investigation. Looking at the correlation of the network metrics with the plays’ number of characters and the normalized degree values might give a first clue. Centrality metrics in co-presence networks typically suffer from a strong correlation with the number of characters (cf. Krautter 2023b; Szemes/Vida 2024, to appear). This seems to be less of an issue for knowledge networks. While degree (Spearman's ρ = 0.43) and especially betweenness centrality (ρ = 0.78) in the co-presence networks have a pretty noticeable correlation with the number of characters, the correlation is less pronounced or not at all detectable in the knowledge networks (degree: ρ = -0.08 betweenness centrality: ρ = 0.36). Furthermore, the normalized degree values show the same pattern as the three other metrics.

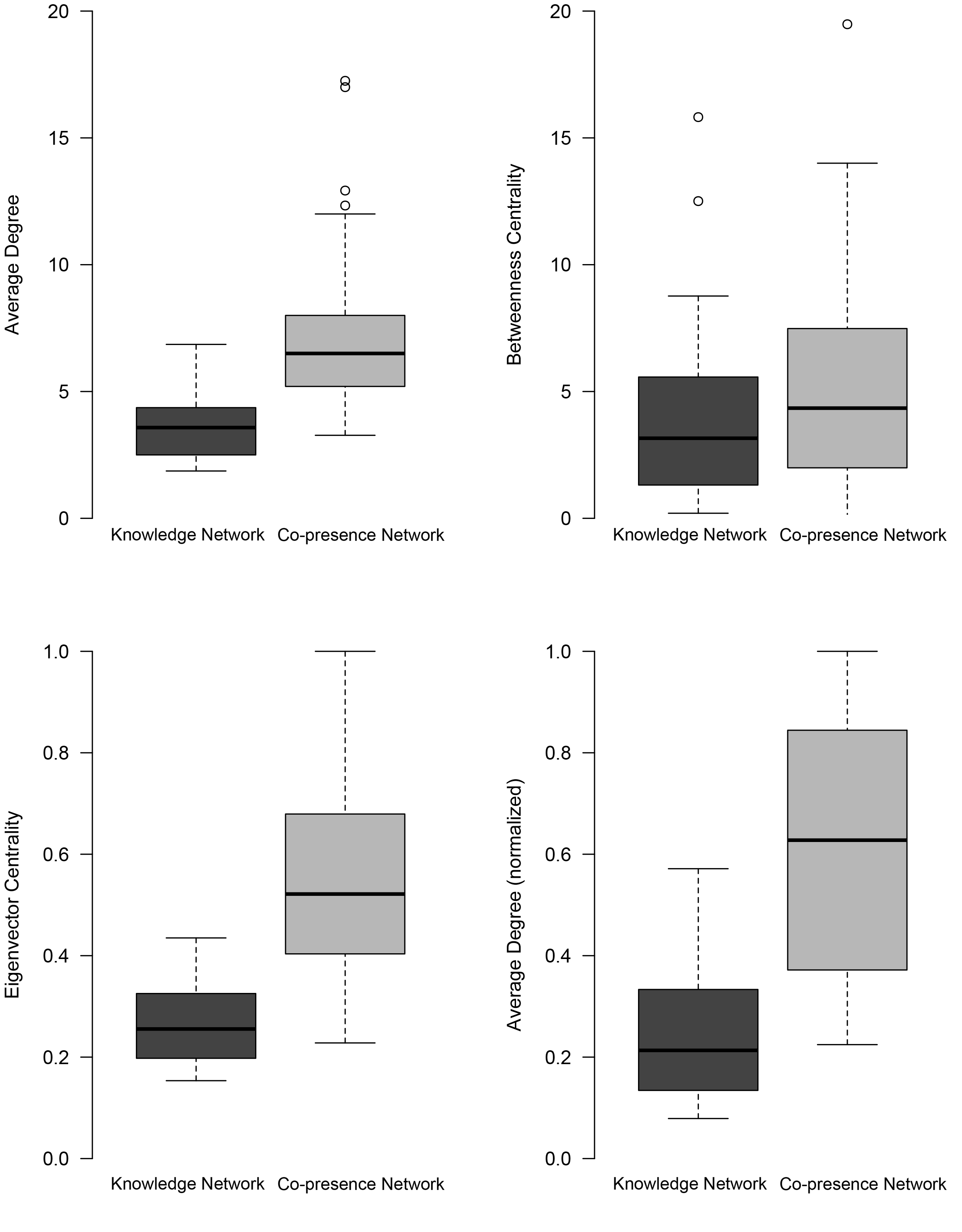
Figure 2: Boxplots of average degree, betweenness centrality, eigenvector centrality and normalized average degree for knowledge and co-presence networks.

5. Knowledge graph: mental representations of character relations

To model our annotation data as a knowledge graph we make use of Neo4j and exemplify the approach with Kleist’s Die Familie Schroffenstein. ⁹ Neo4j is a graph database management system and, correspondingly, stores its data as nodes and edges. In contrast to the network visualized in Figure 1, Neo4j allows for specifying the edges with attributes. In our case, we make use of the relations between SOURCE and TARGET that we have already annotated. This substantiates the visualizations with relevant information and provides a more profound perspective on the modeled plays. Figures 3.1 and 3.2 illustrate the mental representations of Ottokar and Agnes, the two main characters and tragic heroes of the play. For this, we focus on the character relations Ottokar and Agnes learn about during the play. The violet nodes of Ottokar and Agnes represent the characters as they appear in the play. Orange nodes depict the mental representations they have of other characters and their relations. Blue nodes are used for variables, e.g., when a character does not know the identity of someone he meets or hears about. For Agnes and Ottokar, this is especially important, as they both confess each other’s love, without being sure about each other’s identity. As the “identity”-relation between these different mental representations clarifies, both Agnes and Ottokar learn about each other’s identity in the course of the play. A temporal perspective on these mental representations could, thus, further enhance the model we propose, and yield a fruitful vantage point for a “quantitative” close reading.

Figure 3.1: Agnes’ mental representations of character relations modeled in Neo4j.

Figure 3.2: Ottokar’s mental representations of character relations modeled in Neo4j.

6. Conclusion

We have shown two different approaches to model our annotation data of knowledge transmissions in German-language plays. The approaches yield fruitful theoretical and methodological perspectives to deal with research questions in CLS, both from a macroanalytical and a microanalytical perspective. While the true potential for a comprehensive analysis of knowledge transmission throughout German-language drama history still needs a solution for an automatization of the annotation process, experiments with large language models are already promising (cf. Pagel, Pichler, Reiter 2024).

Table 2: List of the calculated knowledge-network metrics of the 30 plays: Char. = number of characters, D. max = maximum degree of a single character, D. avg = average degree the play’s network; equivalent for betweenness and eigenvector centrality.